Skip to contents

cycleTrendR Overview

Source: vignettes/cycleTrendR-overview.Rmd
cycleTrendR-overview.Rmd

Introduction

cycleTrendR provides a unified framework for analyzing time‑series that contain both trend and cyclic components. It supports:

LOESS, GAM, and GAMM trend estimation

Automatic Fourier harmonic selection (AICc/BIC)

Bootstrap confidence intervals (IID or MBB)

Change‑point detection

Lomb–Scargle periodogram for irregular sampling

Rolling‑origin forecasting

Publication‑quality ggplot2 visualizations

This vignette demonstrates the main workflows using simulated data.

Simulated Example Data

We simulate a noisy cyclic signal with irregular sampling:

dates <- as.Date("2020-01-01") + cumsum(sample(1:3, 300, replace = TRUE))
signal <- sin(2*pi*as.numeric(dates)/20) + rnorm(300, 0, 0.3)

LOESS Trend + Automatic Fourier Selection 

res_loess <- adaptive_cycle_trend_analysis(
  signal = signal,
  dates = dates,
  trendmethod = "loess",
  usefourier = TRUE,
  auto_fourier_select = TRUE,
  nboot = 50
)
#> Using original scale.
#> Irregular dates detected: Lomb Scargle + LOESS/GAM(M)
#> Auto seasonality: dominant period approx 20.14 samples -> seasonalfrequency=20
#> loess.as proposed span (criterion=aicc) = 0.944
#> Fourier selection: criterion=AICc -> K=1 (from 0..6)
#> Warning in adaptive_cycle_trend_analysis(signal = signal, dates = dates, :
#> Model-based CI not implemented for this configuration; switching to
#> bootstrapiid.
#> Bootstrap CI (bootstrapiid): 50 resamples
#> Warning in tseries::adf.test(signal, alternative = "stationary"): p-value
#> smaller than printed p-value
#> Warning in tseries::kpss.test(signal, null = "Level"): p-value greater than
#> printed p-value

res_loess$Plot$Trend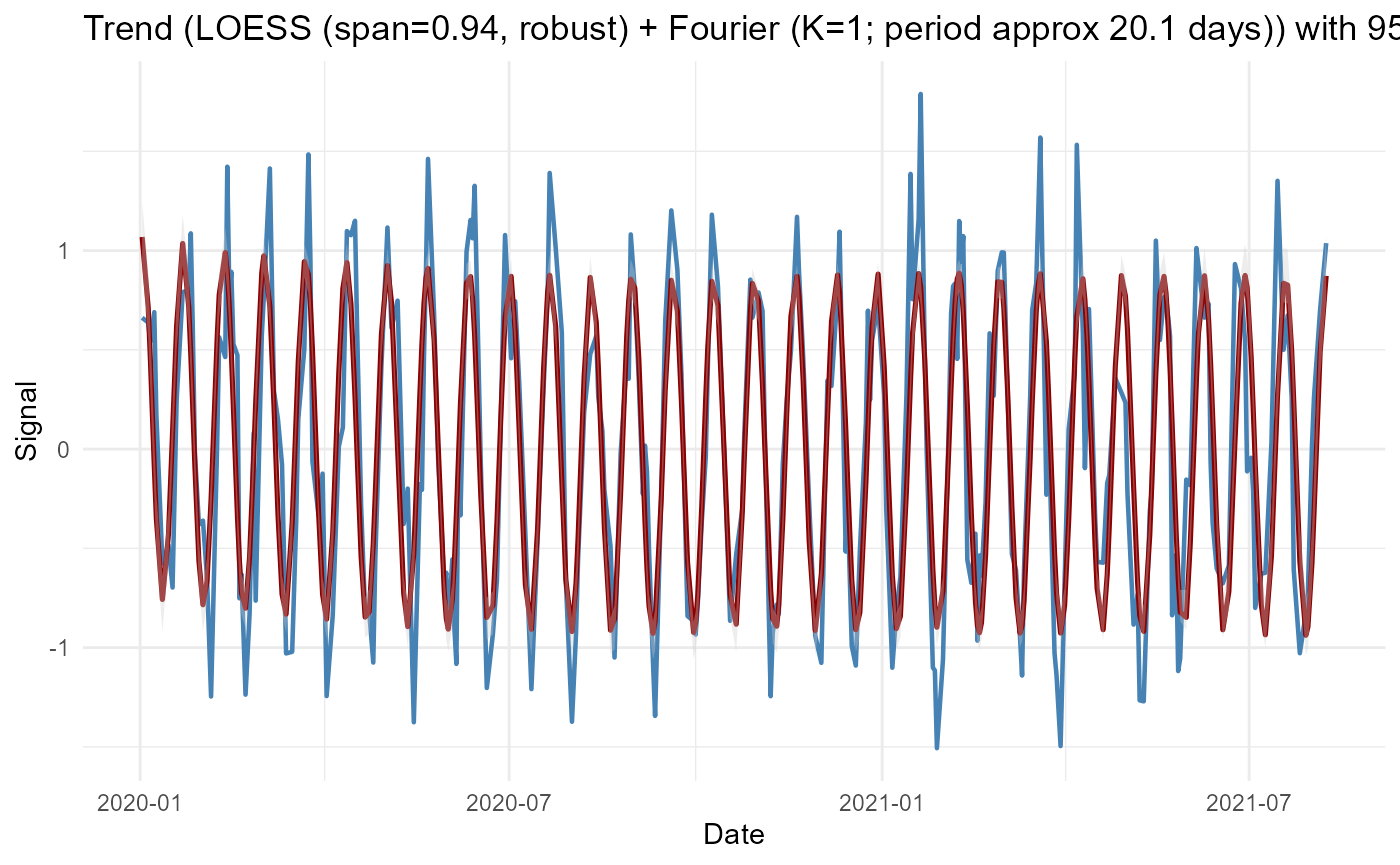

GAM Trend 

res_gam <- adaptive_cycle_trend_analysis(
  signal = signal,
  dates = dates,
  trendmethod = "gam",
  usefourier = TRUE,
  nboot = 50
)
#> Using original scale.
#> Irregular dates detected: Lomb Scargle + LOESS/GAM(M)
#> Auto seasonality: dominant period approx 20.14 samples -> seasonalfrequency=20
#> Fourier selection: criterion=AICc -> K=1 (from 0..6)
#> Warning in adaptive_cycle_trend_analysis(signal = signal, dates = dates, :
#> Model-based CI not implemented for this configuration; switching to
#> bootstrapiid.
#> Bootstrap CI (bootstrapiid): 50 resamples
#> Warning in tseries::adf.test(signal, alternative = "stationary"): p-value
#> smaller than printed p-value
#> Warning in tseries::kpss.test(signal, null = "Level"): p-value greater than
#> printed p-value

res_gam$Plot$Trend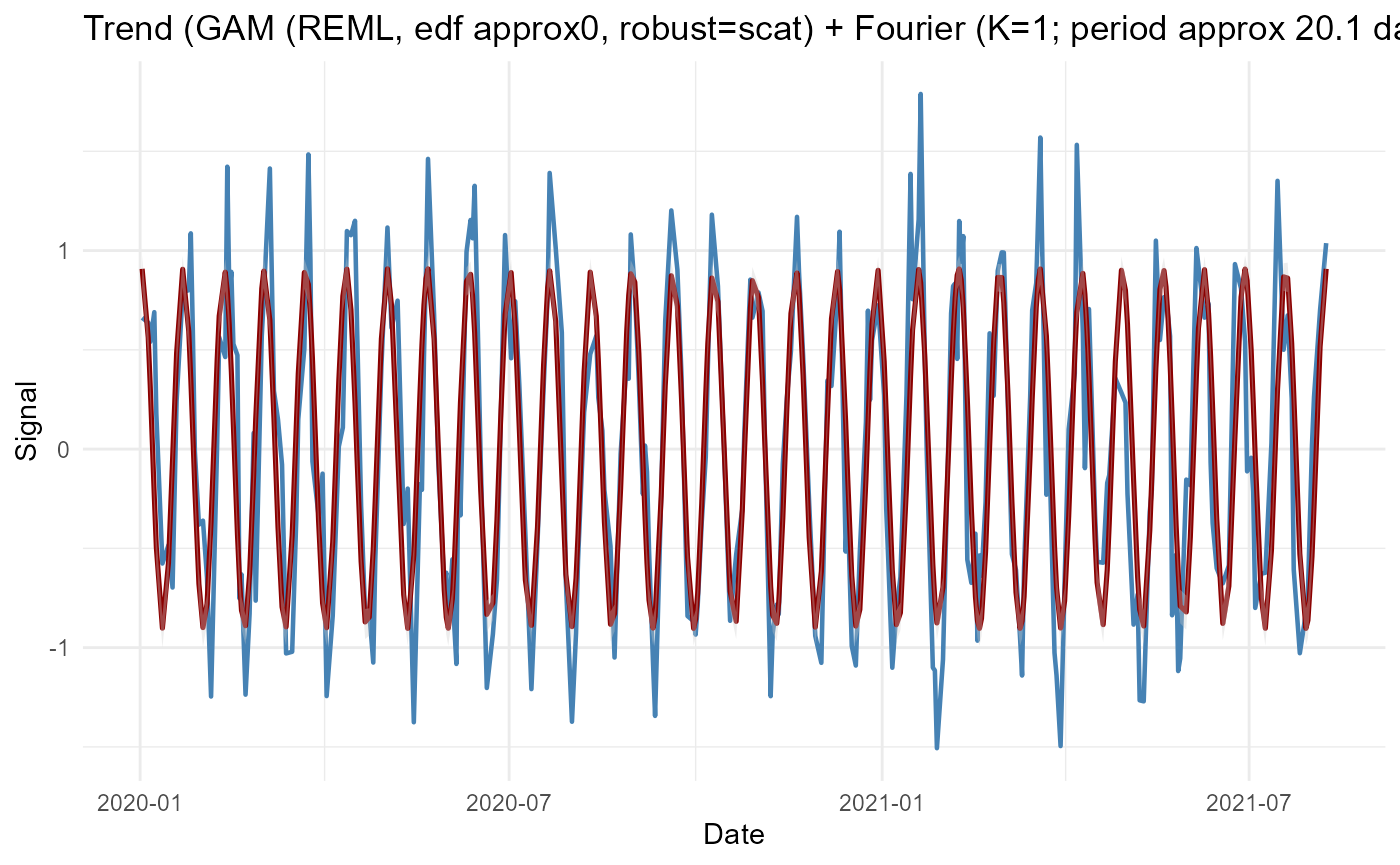

GAMM Trend with Random Effects 

group <- rep(letters[1:4], length.out = length(signal))

res_gamm <- adaptive_cycle_trend_analysis(
  signal = signal,
  dates = dates,
  trendmethod = "gam",
  use_gamm = TRUE,
  group_var = "subject",
  group_values = group,
  usefourier = FALSE,
  nboot = 20
)
#> Using original scale.
#> Irregular dates detected: Lomb Scargle + LOESS/GAM(M)
#> Attached grouping column 'subject' from `group_values`.
#> Converted group_var 'subject' to factor (4 levels).
#> Auto seasonality: dominant period approx 20.14 samples -> seasonalfrequency=20
#> Warning in adaptive_cycle_trend_analysis(signal = signal, dates = dates, :
#> Model-based CI not implemented for this configuration; switching to
#> bootstrapiid.
#> Bootstrap CI (bootstrapiid): 20 resamples
#> Warning in tseries::adf.test(signal, alternative = "stationary"): p-value
#> smaller than printed p-value
#> Warning in tseries::kpss.test(signal, null = "Level"): p-value greater than
#> printed p-value

res_gamm$Plot$Trend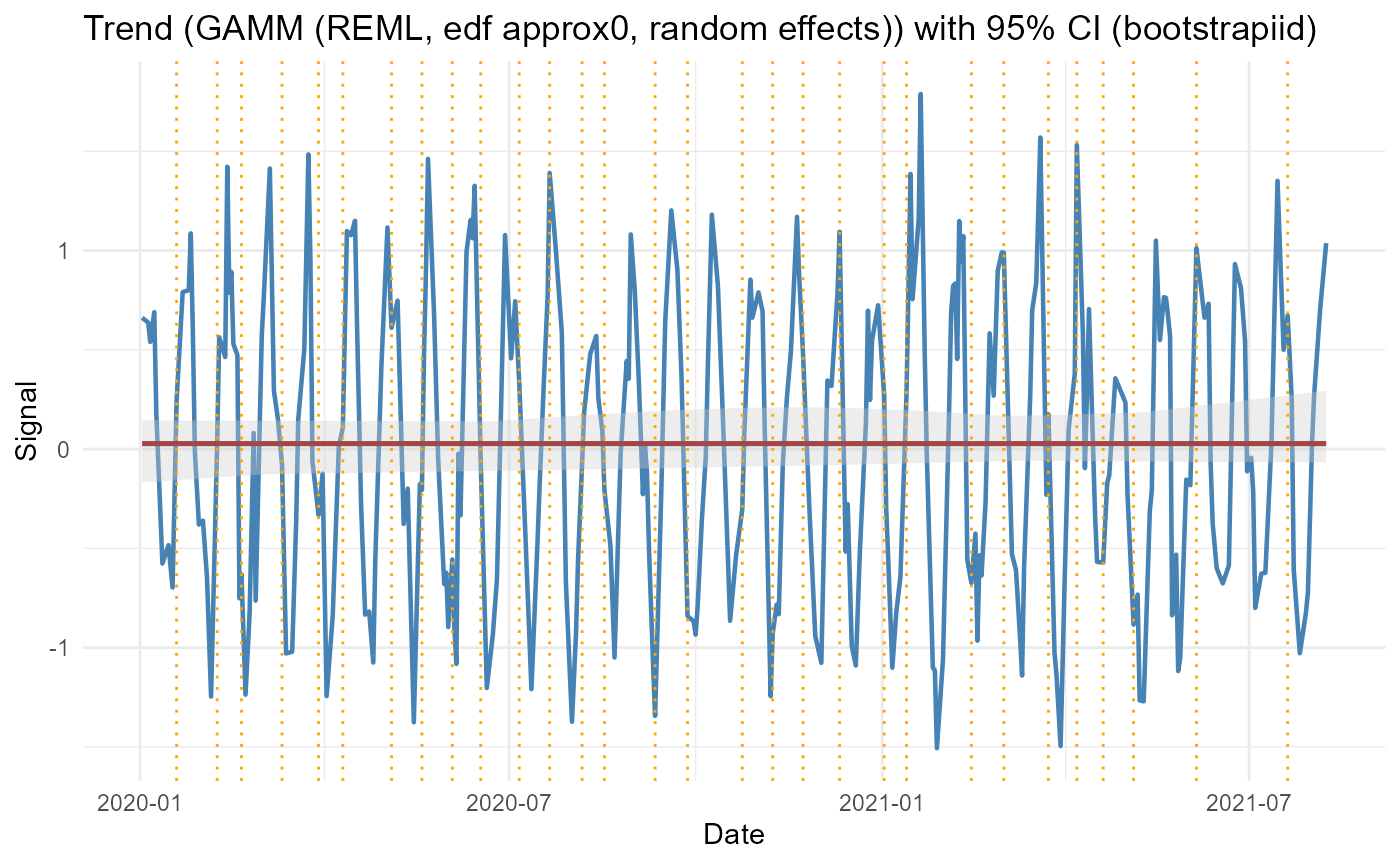

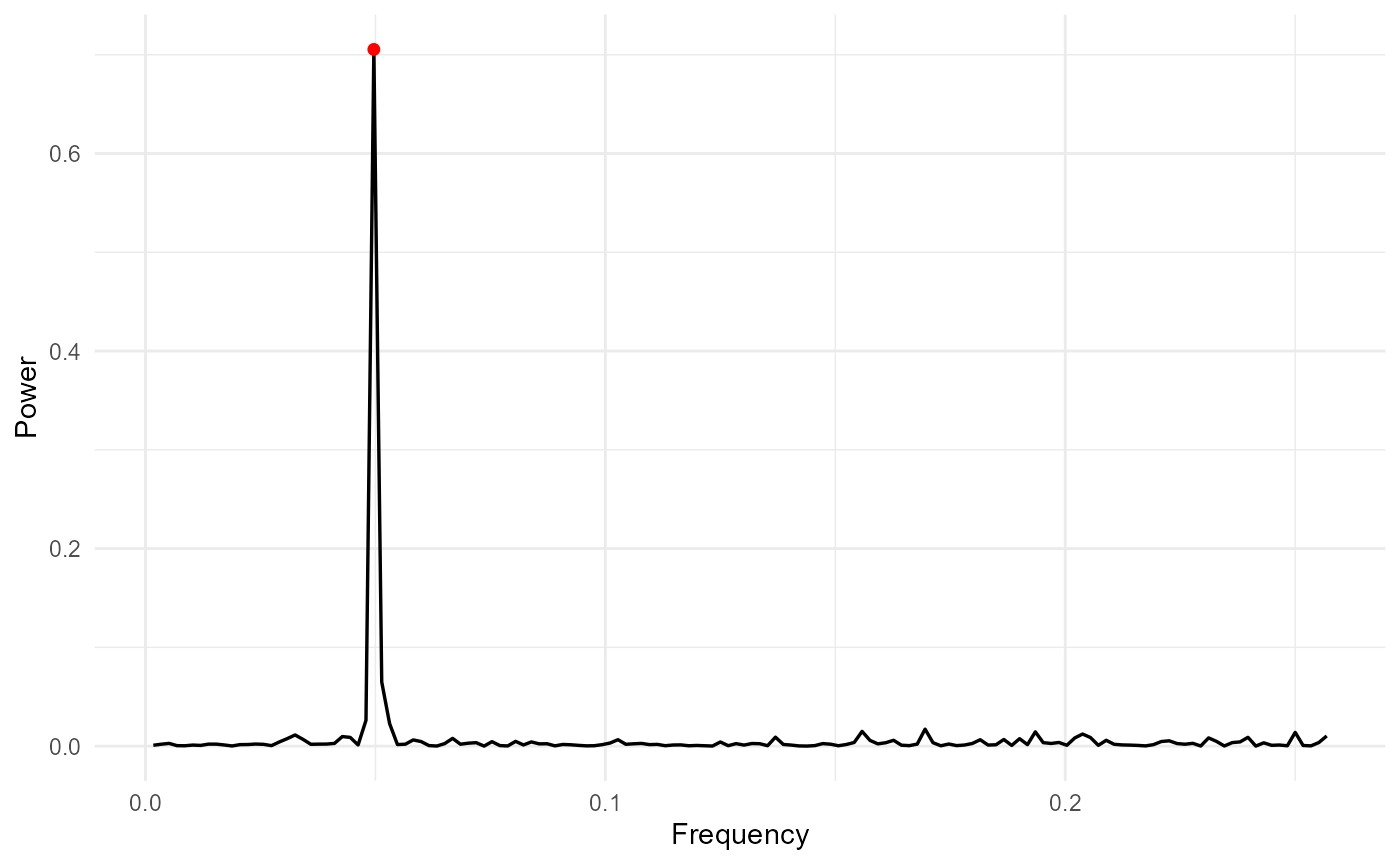
Irregular Sampling + Fourier + Lomb–Scargle

Irregular sampling is detected automatically and the Lomb–Scargle periodogram is used:

  res_irreg <- adaptive_cycle_trend_analysis(
  signal = signal,
  dates = dates,
  trendmethod = "loess",
  usefourier = TRUE,
  auto_fourier_select = TRUE,
  nboot = 50
)
#> Using original scale.
#> Irregular dates detected: Lomb Scargle + LOESS/GAM(M)
#> Auto seasonality: dominant period approx 20.14 samples -> seasonalfrequency=20
#> loess.as proposed span (criterion=aicc) = 0.944
#> Fourier selection: criterion=AICc -> K=1 (from 0..6)
#> Warning in adaptive_cycle_trend_analysis(signal = signal, dates = dates, :
#> Model-based CI not implemented for this configuration; switching to
#> bootstrapiid.
#> Bootstrap CI (bootstrapiid): 50 resamples
#> Warning in tseries::adf.test(signal, alternative = "stationary"): p-value
#> smaller than printed p-value
#> Warning in tseries::kpss.test(signal, null = "Level"): p-value greater than
#> printed p-value

res_irreg$Plot$Spectrum

Change‑Point Detection 

res_loess$ChangePoints
#> Date of length 0

Bootstrap Confidence Intervals 

head(res_loess$CI$lower)
#> [1]  0.9356674  0.5615359  0.3088493 -0.2316584 -0.5025484 -0.9191605
head(res_loess$CI$upper)
#> [1]  1.24514207  0.89025520  0.63385775  0.04906948 -0.22326844 -0.64021793

Conclusion

cycleTrendR provides a flexible and robust toolkit for analyzing complex time‑series with trend and cyclic components, especially when sampling is irregular or noise levels are high. It is suitable for biomedical assay monitoring, environmental signals, and forecasting tasks.